My thoughts / questions on string theory:
1) How were the intitial strings (filaments of energy) detected in the 1970s. Or are the strings theoretical from the get go?
2) Below (in The Basic Elements of String Theory) it says "you can’t construct a string theory without closed strings." My gut tells me that you can't have a theory of everything with open strings. Everything is spherical (eliptical), elastic, and the sum of which always totals 100%.
3) I think of energy filaments as cosmic music (vibrations at frequencies which far exceed our limited perception between 20 and 20,000 hz). However, the music is made with "strings" that are spherical(ish) and connected, not like a guitar string that has a beginning and ending. Cosmic music has always existed and always will, and the concept of time provides the space which allows us to observe the vibration of the strings.
4) As far as quantum gravity, I view gravity as external pressure upon an object, not a pulling inward due to mass. I imagine that objects are dense because of space-time displacement. This occurs when the vibrations of the membranes (musical onion skins that form the closed, spherical(ish) universe) interact with eachother to cause interference (density) or phase cancellation (vacuums) - imagine throwing a handful of pebbles into a lake and watching the patterns (peaks and valleys) of the overlapping concentric circles that form. This view of gravity could be wrong, but it just seems right.
5) Compactification of dimensions - I have a problem with the concept of dimension to begin with. On the grandest of scales (which is the vantage point we are aiming for), the limitations of dimensions keep us from imagining the whole enchilada as a borg-like, single unit.
------
Dimensionless concepts
Constants
Main article: Dimensionless number
The dimensionless constants that arise in the results obtained, such as the C in the Poiseuille's Law problem and the 
in the spring problems discussed above come from a more detailed analysis of the underlying physics, and often arises from integrating some differential equation. Dimensional analysis itself has little to say about these constants, but it is useful to know that they very often have a magnitude of order unity. This observation can allow one to sometimes make "back of the envelope" calculations about the phenomenon of interest, and therefore be able to more efficiently design experiments to measure it, or to judge whether it is important, etc.
in the spring problems discussed above come from a more detailed analysis of the underlying physics, and often arises from integrating some differential equation. Dimensional analysis itself has little to say about these constants, but it is useful to know that they very often have a magnitude of order unity. This observation can allow one to sometimes make "back of the envelope" calculations about the phenomenon of interest, and therefore be able to more efficiently design experiments to measure it, or to judge whether it is important, etc.Formalisms
Paradoxically, dimensional analysis can be a useful tool even if all the parameters in the underlying theory are dimensionless, e.g., lattice models such as the Ising model can be used to study phase transitions and critical phenomena. Such models can be formulated in a purely dimensionless way. As we approach the critical point closer and closer, the distance over which the variables in the lattice model are correlated (the so-called correlation length, 
) becomes larger and larger. Now, the correlation length is the relevant length scale related to critical phenomena, so one can, e.g., surmize on "dimensional grounds" that the non-analytical part of the free energy per lattice site should be 
where 
is the dimension of the lattice.
) becomes larger and larger. Now, the correlation length is the relevant length scale related to critical phenomena, so one can, e.g., surmize on "dimensional grounds" that the non-analytical part of the free energy per lattice site should be where is the dimension of the lattice.
It has been argued by some physicists, e.g., Michael Duff,[4][6] that the laws of physics are inherently dimensionless. The fact that we have assigned incompatible dimensions to Length, Time and Mass is, according to this point of view, just a matter of convention, borne out of the fact that before the advent of modern physics, there was no way to relate mass, length, and time to each other. The three independent dimensionful constants: c, ħ, and G, in the fundamental equations of physics must then be seen as mere conversion factors to convert Mass, Time and Length into each other.
Just as in the case of critical properties of lattice models, one can recover the results of dimensional analysis in the appropriate scaling limit; e.g., dimensional analysis in mechanics can be derived by reinserting the constants ħ, c, and G (but we can now consider them to be dimensionless) and demanding that a nonsingular relation between quantities exists in the limit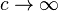 
, 
and 
. In problems involving a gravitational field the latter limit should be taken such that the field stays finite.
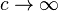, and . In problems involving a gravitational field the latter limit should be taken such that the field stays finite.
----------------------------
http://www.dummies.com/how-to/
The Basic Elements of String Theory
Five key ideas are at the heart of string theory. Become familiar with these key elements of string theory right off the bat. Read on for the very basics of these five ideas of string theory in the sections below.
Strings and membranes
When the theory was originally developed in the 1970s, the filaments of energy in string theory were considered to be 1-dimensional objects: strings. (One-dimensional indicates that a string has only one dimension, length, as opposed to say a square, which has both length and height dimensions.)
These strings came in two forms — closed strings and open strings. An open string has ends that don’t touch each other, while a closed string is a loop with no open end. It was eventually found that these early strings, called Type I strings, could go through five basic types of interactions, as shown this figure.
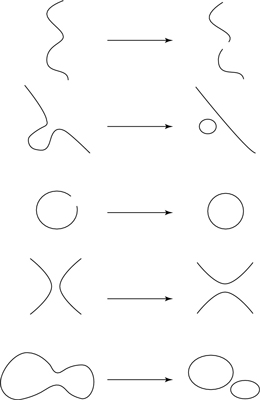
Type I strings can go through five fundamental interactions, based on different ways of joining and splitting.
The interactions are based on a string’s ability to have ends join and split apart. Because the ends of open strings can join together to form closed strings, you can’t construct a string theory without closed strings.
This proved to be important, because the closed strings have properties that make physicists believe they might describe gravity. Instead of just being a theory of matter particles, physicists began to realize that string theory may just be able to explain gravity and the behavior of particles.
Over the years, it was discovered that the theory required objects other than just strings. These objects can be seen as sheets, or branes. Strings can attach at one or both ends to these branes. A 2-dimensional brane (called a 2-brane) is shown in this figure.
In string theory, strings attach themselves to branes.
Quantum gravity
Modern physics has two basic scientific laws: quantum physics and general relativity. These two scientific laws represent radically different fields of study. Quantum physics studies the very smallest objects in nature, while relativity tends to study nature on the scale of planets, galaxies, and the universe as a whole. (Obviously, gravity affects small particles too, and relativity accounts for this as well.) Theories that attempt to unify the two theories are theories of quantum gravity, and the most promising of all such theories today is string theory.
Unification of forces
Hand-in-hand with the question of quantum gravity, string theory attempts to unify the four forces in the universe — electromagnetic force, the strong nuclear force, the weak nuclear force, and gravity — together into one unified theory. In our universe, these fundamental forces appear as four different phenomena, but string theorists believe that in the early universe (when there were incredibly high energy levels) these forces are all described by strings interacting with each other.
Supersymmetry
All particles in the universe can be divided into two types: bosons and fermions. String theory predicts that a type of connection, calledsupersymmetry, exists between these two particle types. Under supersymmetry, a fermion must exist for every boson and vice versa. Unfortunately, experiments have not yet detected these extra particles.
Supersymmetry is a specific mathematical relationship between certain elements of physics equations. It was discovered outside of string theory, although its incorporation into string theory transformed the theory into supersymmetric string theory (or superstring theory) in the mid-1970s.
Supersymmetry vastly simplifies string theory’s equations by allowing certain terms to cancel out. Without supersymmetry, the equations result in physical inconsistencies, such as infinite values and imaginary energy levels.
Because scientists haven’t observed the particles predicted by supersymmetry, this is still a theoretical assumption. Many physicists believe that the reason no one has observed the particles is because it takes a lot of energy to generate them. (Energy is related to mass by Einstein’s famous E = mc2 equation, so it takes energy to create a particle.) They may have existed in the early universe, but as the universe cooled off and energy spread out after the big bang, these particles would have collapsed into the lower-energy states that we observe today. (We may not think of our current universe as particularly low energy, but compared to the intense heat of the first few moments after the big bang, it certainly is.)
Scientists hope that astronomical observations or experiments with particle accelerators will uncover some of these higher-energy supersymmetric particles, providing support for this prediction of string theory.
Extra dimensions
Another mathematical result of string theory is that the theory only makes sense in a world with more than three space dimensions! (Our universe has three dimensions of space — left/right, up/down, and front/back.) Two possible explanations currently exist for the location of the extra dimensions:
- The extra space dimensions (generally six of them) are curled up (compactified, in string theory terminology) to incredibly small sizes, so we never perceive them.
- We are stuck on a 3-dimensional brane, and the extra dimensions extend off of it and are inaccessible to us.
A major area of research among string theorists is on mathematical models of how these extra dimensions could be related to our own. Some of these recent results have predicted that scientists may soon be able to detect these extra dimensions (if they exist) in upcoming experiments, because they may be larger than previously expected.
No comments:
Post a Comment